A. Persamaan Dan Pertidaksamaan Linear
1). Persamaan Linear
Persamaan Adalah Kalimat Terbuka Yang Memuat Tanda “Sama Dengan” Atau “=”. Sementara Itu, Yang Dimaksud Kalimat Terbuka Adalah Kalimat Yang Belum Diketahui Nilai Kebenarannya.
Persamaan Linear Adalah Suatu Persamaan Yang Variabelnya Memiliki Pangkat Tepat Satu
Persamaan Adalah Kalimat Terbuka Yang Memuat Tanda “Sama Dengan” Atau “=”. Sementara Itu, Yang Dimaksud Kalimat Terbuka Adalah Kalimat Yang Belum Diketahui Nilai Kebenarannya.
Persamaan Linear Adalah Suatu Persamaan Yang Variabelnya Memiliki Pangkat Tepat Satu
a.Persamaan Linear Satu Variabel
Contoh :
- 2x + 10 = 0 (variabel : x)
- 2t = 14 (variabel : t)
b. Persamaan Linear Dua Variabel
Contoh :
- x + 3y = 9 (variabel : x dan y)
- 2m – 3n = 15 (variabel : m dan n)
c. Persamaan Linear 3 Variabel
Contoh :
- 2x + y – 3z = 20 (variabel : x , y , dan z)
- 2p – 5q + 2r = -3 (variabel : p , q , dan r)
Persamaan Linear Memiliki Beberapa Sifat Yang Perlu Diperhatikan Dalam Menyelesaikannya. Berikut Adalah SIfat Persamaan Linear Satu Variabel :
SIFAT 1 : Nilai Persamaan Tidak Berubah Jika Pada Ruas Kiri Dan Kanan Ditambah/Dikurangi Dengan Bilangan Yang Sama.
SIFAT 2 : Nilai Persamaan Tidak Berubah Jika Pada Ryas Kiri Dan Kanan Dikali/Dibagi Dengan Bilangan Tak Nol Yang Sama
2. Pertidaksamaan Linear
Pertidaksamaan adalah kalimat terbuka yang menggunakan tanda <, > , ≤ , ≥ . Sedangkan Pertidaksamaan Linear Adalah Suatu Pertidaksamaan Yang Mempunyai Variabel Dengan Peringkat Tepat Satu.
a. Pertidaksamaan Linear satu variabel
- 2x = 10 > 0 (variabel : x)
- 2t ≤ 14 (variabel : t)
b. Pertidaksamaan Linear dua variabel
- x + 3y ≤ 9 (variabel : x dan y)
- 2p > 3q + 15 (variabel : p dan q)
Penyelesaian Pertidaksamaan adalah konstanta pengganti variabel yang menyebabkan suatu pertidaksamaan menjadi kalimat yang benar.
Sifat – Sifat Pertidaksamaan Linear :
SIFAT 1 : Suatu pertidaksamaan tidak berubah tandanya jika kedua ruas pertidaksamaan ditambah atau dikurangi dengan bilangan yang sama misal x > y maka x + a > y + a
SIFAT 2 : Suatu pertidaksamaan tidak berubah tandanya jika kedua ruas dikali atau dibagi dengan bilangan positif yang sama, misalnya x ≤ y maka a .x ≤ y. a dengan a > 0
SIFAT 3 : Suatu pertidaksamaan akan berubah tandanya jika kedua ruas dikali atau dibagi dengan bilangan negatif yang sama misal x ≤ y maka –x a ≥ -y a (berubah tanda karena kedua ruas dikali dengan bilangan negatif yang sama) misal x ≤ y maka (berubah tanda karena kedua ruas dibagi dengan bilangan negatif yang sama.)
B. Nilai Mutlak
Nilai mutlak adalah jarak pada garis bilangan real antara bilangan yang dimaksud dengan dengan nol.
untuk  bilangan real didefinisikan
bilangan real didefinisikan 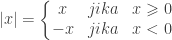
Contoh:
Sifat Sifat Nilai Mutlak
, (ketaksamaan segitiga)
atau
Contoh Soal Dan Pembahasannya
1). Nilai x yang memenuhi persamaan  adalah ….
adalah ….
2). Sederhanakan bentuk pertidaksamaan : 11x + 2 < 2𝑥 + 39 + 2(x + 1)
11x + 2 < 2𝑥 + 39 + 2(x + 1)
11x + 2 < 2x + 49 + 2x + 2
11x + 2 < 4x + 51
11x - 4x < 51 - 2
7x < 49
Tidak ada komentar:
Posting Komentar